[Nature of Code] Chapter 0.0 : Randomness
2024.01.07

난수 생성은 우연에 맡기기엔 너무 중요하다 - Robert R. Coveyou
이제 우리는 시작점에 와있다. 자바스크립트로 프로그래밍한지(또는 수학을 해본 지) 꽤 오래 되었다면, 이 챕터에서 computational thinking에 다시 익숙해질 수 있을 것이다. coding-of-nature에 대한 여정을 시작하기 위해, 시뮬레이션 프로그래밍을 위한 몇가지 기본 도구인 난수, 랜덤분포, 노이즈를 소개한다. 이 책을 구성하는 첫번째 (0번째!) 요소로 - 앞으로 펼처질 가능성에 대한 복습과 관문이라고 생각하면 된다.
1장에서는, 벡터의 개념과 벡터가 어떻게 이 책 전체에서 모션 시뮬레이션의 구성요소로 사용되는지 설명할 것이다. 하지만 그 전에, 디지털 캔버스에서 무언가가 움직인다는 것이 무엇을 의미하는지 생각해보자. 가장 잘 알려져 있고 간단한 모션 시뮬레이션인 random walk부터 시작할 것 이다.
Random Walks
Random Walks (무작위 행보)
시간에 따라 무작위로 움직이는 경로를 나타내는 수학적인 개념.
평균대 한 가운데 서 있다고 상상해보자. 10초마다 동전을 던진다. 앞면이면, 한 걸음 나아간다. 뒷면이면, 한 걸��음 물러난다. 이것이 random walk로, 일련의 무작위 단계들로 정의되는 경로이다. 이 균형대를 (조심스럽게) 밟고 바닥으로 내려오면, random walk를 1차원(앞뒤로만 이동)에서 2차원(앞, 뒤, 왼, 오로 이동)으로 확장할 수 있다. 이제 4가지 가능성이 있으므로, 다음 스텝을 결정하려면 같은 동전을 두 번 던져야 한다:
| Flip 1 | Flip 2 | Result |
|---|---|---|
| 앞 | 앞 | 앞으로 이동 |
| 앞 | 뒤 | 오른쪽으로 이동 |
| 뒤 | 앞 | 왼쪽으로 이동 |
| 뒤 | 뒤 | 뒤로 이동 |
이는 정교하지 않은 알고리즘처럼 보일 수 있지만, random walk를 사용하면 기체 속 분자의 움직임부터 동물의 먹이 찾기, 카지노에서 하루를 보내는 겜블러의 행동까지 현실 세계에서 일어나는 모든 종류의 현상을 모델링할 수 있다. random walk는 다음 3가지 이유에서 우리의 목적을 시작하기에 완벽한 곳이다:
- 우리는 이 책의 중심이 되는 프로그래밍 개념인 객체 지향 프로그래밍 (OOP)를 살펴볼 것이다. 우리가 만들고자 하는 random walk는 객체 지향 디자인을 사용하여 컴퓨터 그래픽 캔버스에서 움직이는 사물을 만들기 위한 템플릿 역할을 할 것이다.
- Random walk는 이 책 전체에서 반복해서 던질 2가지 질문을 불러일으킨다: “사물의 동작을 지배하는 규칙을 어떻게 정의할 것인가?” 그리고, “그 규칙을 코드로 어떻게 구현할 것인가?”
- 이 책의 프로젝트를 진행하려면 무작위성, 확률, Perlin 노이즈에 대한 기본적인 이해가 필요하다. Random walk를 통해 나중에 유용하게 사용할 수 있는 핵심 사항을 보여줄 수 있다.
Perlin noise
컴퓨터 그래픽스와 시뮬레이션 등에서 사용되는 확률적인 기술로, 자연 현상의 무작위성을 모델링하는 데 사용된다. 컴퓨터 그래픽스에서 현실적이고 자연스러운 텍스처, 지형, 파동 등을 생성하는 데 주로 활용된다.
먼저 random walk를 할 수 있는 Walker 객체를 생성하는 Walker 클래스를 코딩하여 약간의 OOP를 살펴볼 것이다.
이는 피상적인 검토일 뿐이다.
OOP를 사용해본 적이 없다면, 좀 더 포괄적인 내용을 원할 수 있으므로; 여기서 멈추고 ES6 클래스의 기본 사항에 대한 비디오 튜토리얼을 살펴보는 것을 추천한다.
The Random Walker Class
전체 코드
let walker;
function setup() {
createCanvas(640, 240);
walker = new Walker();
background(255);
}
function draw() {
walker.step();
walker.show();
}
class Walker {
constructor() {
this.x = width / 2;
this.y = height / 2;
}
show() {
stroke(0);
point(this.x, this.y);
}
step() {
const choice = floor(random(4));
if (choice == 0) {
this.x++;
} else if (choice == 1) {
this.x--;
} else if (choice == 2) {
this.y++;
} else {
this.y--;
}
}
}자바스크립트에서 객체는 데이터와 기능을 모두 가진 엔티티이다.
이 경우, Walker 객체는 캔버스에서의 자신의 위치에 대한 데이터와, 스스로를 그리거나 한걸음 나아가는 등의 기능이 있어야 한다.
클래스는 객체의 실제 인스턴스를 구축하기 위한 템플릿이다.
클래스를 쿠키 커터로, 객체를 쿠키 자체로 생각해보자.
Walker 객체를 생성하기 위해, Walker 클래스를 정의하는 것부터 시작할 것이다.
walker는 오직 x 위치에 대한 숫자와 y위치에 대한 숫자 2가지 데이터만 필요하다.
2가지 데이터를 캔버스의 중앙으로 초기화하여 객체의 시작 위치를 설정하자.
이 작업은 클래스의 생성자 함수인 constructor()에서 수행할 수 있다.
생성자는 객체의 setup() 함수라고 생각하면 된다. 이 함수는 setup()이 스케치 전체에 대해 수행하는 것과 마찬가지로, 객체의 초기 속성을 정의하는 역할을 한다.
class Walker {
// 객체는 자신이 초기화되는 constructor를 가진다.
constructor() {
// 객체는 데이터를 가진다.
this.x = width / 2;
this.y = height / 2;
}
}새로 생성된 객체 자체에 속성을 첨부하기 위해 this 키워드를 사용하는 것을 확인해라 : this.x 와 this.y.
데이터 외에도, 클래스는 기능으로 정의될 수 있다.
이 예제에서, Walker 객체는 OOP 컨텍스트에서 method라 불리는 2가지 함수가 있다.
메소드는 본질적으로 함수이지만, 메소드는 클래스 내부에 정의되므로 객체나 클래스와 관련이 있지만 함수는 그렇지 않다는 점에서 차이가 있다.
function 키워드는 좋은 단서이다. 독립된 함수를 정의할 때 이를 볼 수 있지만, 클래스 내부에서는 보이지 않는다.
이 책에서 용어를 일관성있게 사용하려고 최대한 노력할 것 이지만, 프로그래머들에게 function 과 method 용어를 혼용에서 사용하는 것은 일반적이다.
첫번째 메서드인 show()는 객체를 그리는 코드가 포함되어 있다(검은 점으로). 다시 한번 강조하지만, 객체의 속성(변수)를 참조할때는 this.를 잊지마라.
// 객체는 메소드들을 가진다.
show() {
stroke(0);
point(this.x, this.y);
}다음 메서드인 step()은 Walker 객체에 한 걸음씩 걸으라고 지시한다. 여기서부터 좀 더 흥미로워진다.
바닥에서 임의의 방향으로 한 걸음씩 걸었던 것을 기억하는가?
이제 그 바닥을 표현하기 위해 p5.js 캔버스를 사용할것이다. 여기에는 4가지 가능한 단계가 있다.
오른쪽으로 한 걸음은 x++로 x를 증가시켜 시뮬레이션할 수 있고, 왼쪽은 x—-로 x를 감소시켜, 한 픽셀을 올려서(y—-) 앞으로, 한 픽셀을 내려서(y++) 뒤로 시뮬레이션할 수 있다.
하지만 이 4가지 선택지 중에서 코드는 어떻게 선택할 수 있을까?
앞서 2개의 동전을 던질 수 있다고 말했다.
그러나 p5.js에서는, 옵션 리스트에서 무작위로 선택하고 싶은 경우 간단히 random() 함수를 이용해 난수를 생성하면 된다.
이 함수는 원하는 범위 내에서 임의의 부동 소수점(십진수)값을 선택한다. 여기서는 4를 사용하여 0 ~ 4까지의 범위를 나타낸다.
let choice = floor(random(4));변수 choice를 선언하고, floor()를 사용하여 임의의 부동소수점 숫자에서 소수 자릿수를 제거하여 임의의 정수를 할당한다.
엄밀히 말하면, random(4)로 생성된 숫자는 0 (포함)에서 4 (제외)의 범위 내��에 있으므로, 실제로는 4.0이 될 수 없다.
이 함수가 생성할 수 있는 가장 높은 숫자는 4 바로 아래 - 3.999999999(자바스크립트가 허용하는 만큼의 9를 포함)이며, 이 경우 floor()는 소수점을 제거하여 3으로 잘라낸다.
따라서, choice에 0, 1, 2, 또는 3의 값을 효과적으로 할당했다.
Coding Conventions
자바스크립트에서, 변수는 let 또는 const를 사용하여 선언할 수 있다.
일반적인 접근방식은 모든 변수를 const로 선언하고 필요할 때 let으로
변경하는 것이다. 첫번째 예제에서, step()을 호출할 때 마다 새로운 값이
재할당되지 않으므로 choice를 선언할 때 const가 적절할 것이다. 이러한
차별화도 중요하지만, 나는 p5.js 예제 컨벤션을 따르고 모든 변수를 let으로
선언하기로 선택했다.
자바스크립트에서 const와 let 모두 중요함을 알 고 있다. 하지만
초보자에게는 이러한 구분이 산만하고 혼란스러울 수 있다. 이 주제를 더 자세히
살펴보고, 자신의 스케치에서 변수를 가장 잘 선언하는 방법을 스스로 결정하기를
바란다. 자세한 내용은 p5.js 깃허브 레포에서 이슈 #3877과 관련된 discussion을
읽어봐라. 나는 또한 자바스크립트의 엄격한 등호(===) 연산자(및 그 반대인
!==)를 사용하기로 선택했다. 이 불리언 연산자는 값과 타입의 동일성을 모두
확인한다. 예를들어, 3 === ‘3’은 비슷해 보이지만 타입이 다르기 때문에 (숫자
vs 문자열) false로 평가된다. 반면 3 == ‘3’에 느슨한 등호 연산자(==)를
사용하면 두 다른 타입이 비교가능한 타입으로 변환되기 ��때문에 true로
평가된다. 느슨한 비교도 종종 잘 작동하지만, 때떄로 예기치 못한 결과를 가져올
수 있기 때문에 === 가 더 안전한 선택일 수 있다.
다음으로, walker는 어떤 난수가 선택되었는지에 따라 적절한 걸음(왼, 오, 위, 아래)을 취한다. 다음은 Walker 클래스를 마무리하는 전체 step() 메서드이다.
step() {
let choice = floor(random(4));
if (choice === 0) {
this.x++;
} else if (choice === 1) {
this.x--;
} else if (choice === 2) {
this.y++;
} else {
this.y--;
}
}이제 클래스를 작성했으니, 스케치에서 실제 Walker 객체를 만들 차례이다. 하나의 random walk를 모델링한다고 가정하고, 하나의 전역 변수로 시작해보자:
let walker;그런 다음 new 연산자로 클래스 이름을 참조하여 setup() 에서 객체를 생성한다.
// p5.js에서 setup()은 스케치가 시작될 때 한번 실행된다.
function setup() {
createCanvas(640, 240);
// walker 생성
walker = new Walker();
background(255);
}마지막으로, draw()를 호출할 때 마다, walker는 한 걸음씩 걸으며 점을 그린다.
// draw()를 계속 반복한다
function draw() {
walker.step();
walker.show();
}draw()를 통해 매번 계속 배경을 지우는게 아니라, setup()에서 한 번만 배경을 그리기 때문에 캔버스에서 random walk의 흔적을 볼 수 있다.
Example 0.1: A Traditional Random Walk

random walker의 몇가지를 조정할 수 있다.
우선, 이 Walker 객체의 걸음은 4가지 옵션: 위, 아래, 왼쪽, 오른쪽으로 제한된다. 하지만 캔버스의 픽셀은 대각선을 포함하여 8개의 가능한 이웃을 가질 수 있다.
같은 위치에 머무르는 9번쨰 가능성도 옵션이 될 수 있다.

인접한 픽셀로 이동할 수 있는(또는 제자리에 머무르는) Walker 객체를 구현하려면, 0에서 8까지의 숫자를 선택해야한다(9가지 선택 가능).
그러나 또 다르게 코드를 작성하는 방법은, x축을 따라 3가지 가능한 단계(-1, 0, 1), y축을 따라 3가지 가능한 단계(-1, 0, 1)을 고르는 것이다:
step(){
// -1, 0 또는 1
let xstep = floor(random(3)) - 1;
let ystep = floor(random(3)) - 1;
this.x += xstep;
this.y += ystep;
}한 걸음 더 나아가, floor()를 없애고 random() 함수의 원래 부동 소수점 숫자를 사용하여 -1에서 1까지 가능한 단계의 연속 범위를 만들 수 있다.
step(){
// -1.0 부터 1.0까지의 랜덤 부동 소수점 숫자
let xstep = random(-1, 1);
let ystep = random(-1, 1);
this.x += xstep;
this.y += ystep;
}전통적인 random walk에 대한 모든 변형에는 한가지 공통점이 있다: 어느 시점에서든, walker가 주어진 방향으로 한 걸음 나아갈 확률은 walker가 다른 방향으로 한 걸음 나아갈 확률과 같다는 점이다. 즉, 가능한 걸음이 4가지인 경우 walker가 주어진 방향으로 나아갈 확률은 1/4 (25%)이다. 가능한 방향이 9가지인 경우에는 1/9 (약 11.1%) 확률이다.
간단하게, 이것이 random() 함수가 어떻게 동작하는지이다. p5.js의 난수 생성기(백그라운에서 동작)는 숫자의 uniform distribution을 생성한다.
난수가 선택될때마다 각 횟수를 카운트하고 이 값들을 그래프로 표시하여 이 분포를 테스트할 수 있다.
uniform distribution 균일분포
각각의 가능한 결과가 동일한 확률로 발생하는 확률 분포를 나타낸다. 이는 각 값이 나타날 확률이 균등하게 분포되어 있다는 것을 의미한다. 예를 들어, 1에서 6까지의 주사위를 던질 때, 각 숫자가 나타날 확률은 1/6으로 동일하므로 주사위의 결과는 균일 분포를 따른다.
Example 0.2: A Random-Number Distribution
// 특정 난수가 얼마나 선택되었는지 기록하기 위한 배열
let randomCounts = [];
let total = 20;
function setup() {
createCanvas(640, 240);
for (let i = 0; i < total; i++) {
randomCounts[i] = 0;
}
}
function draw() {
background(255);
// 난수를 선택하고 카운트를 증가시킨다.
let index = floor(random(randomCounts.length));
randomCounts[index]++;
stroke(0);
fill(127);
let w = width / randomCounts.length;
// 결과를 그래프로 표시한다.
for (let x = 0; x < randomCounts.length; x++) {
rect(x * w, height - randomCounts[x], w - 1, randomCounts[x]);
}
}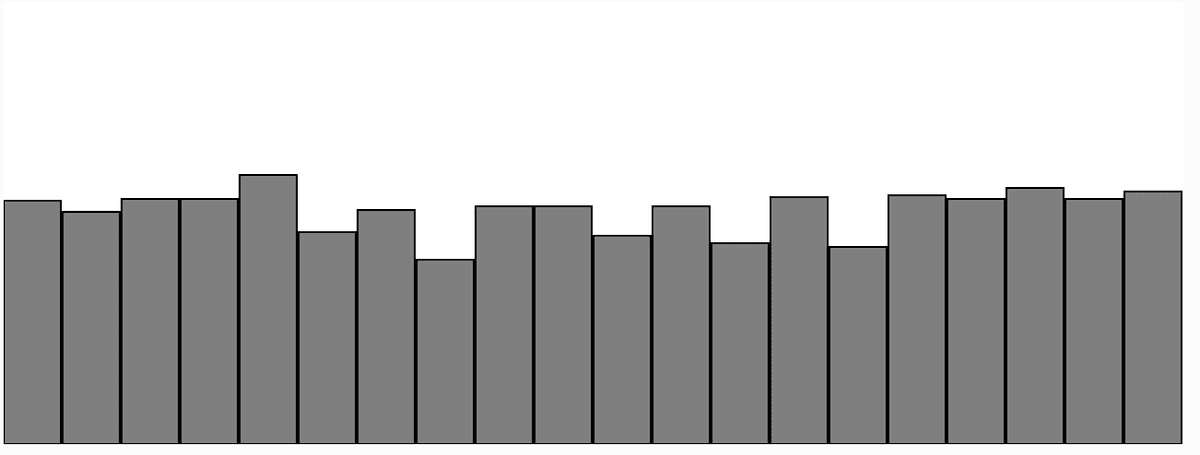
그래프의 각 막대의 높이가 조금씩 다르다는 것을 알 수 있다. 샘플 크기(선택된 난수의 수)가 작기 때문에, 특정 숫자가 다른 숫자보다 더 자주 선택되어 간혹 불일치가 나타날 수 있다. 시간이 지나고, 좋은 난수 생성기를 사용하면 이 분포가 균일해질 것이다.
Pseudorandom Numbers ( 의사 난수 )
Pseudorandom Numbers 의사 난수
컴퓨터 프로그램에서 생성된 수열로, 특정 초기값(seed)에 대한 알고리즘에 따라 계산되어 보이기에는 무작위처럼 보이는 수열. 이것들은 실제로 완전한 무작위 수가 아니라, 초기값과 알고리즘에 의해 결정되는 결정론적인 수열이다.
random() 함수의 난수는 진짜 랜덤이 아니다. 대신 단순히 무작위성을 시뮬레이션하는 수학 함수의 결과이기 때문에 의사 난수이다.
이 함수는 시간이 지날수록 패턴을 생성하므로 무작위로 보이지 않게 된다. 그러나 그 기간이 너무 길기 때문에, 이 책의 예제에서는 random()도 충분히 무작위이다.
Exercise 0.1
아래와 오른쪽으로 이동하는 경향이 더 큰 random walker를 생성해라. (솔루션은 다음 섹션에서 설명)
Probability and Nonuniform Distributions
균일분포는 디자인 문제 - 특히 유기적이거나 자연스러운 시뮬레이션을 구축하는것과 관련된 문제에 가장 신중한 해결책이 아닌 경우가 많다.
그러나 몇가지 트릭과 함께, random() 함수를 통해 일부 결과가 다른 결과보다 더 높은 확률로 나타나는 난수의 비균등 분포를 생성할 수 있다.
이러한 유형의 분포는 더 흥미롭고, 자연스러워보이는 결과를 얻을 수 있다.
p5.js로 처음 프로그래밍을 시작했을 때를 생각해�보자. 아마도 화면에 많은 원을 그리고 싶어서, “아 알겠다! 모든 원들을 임의의 위치에 임의의 크기와 색상으로 그려야지!” 라고 생각했을 것이다. 컴퓨터 그래픽의 기초를 배울때 시스템에 무작위성을 부여하는 것은 매우 합리적인 출발점이지만, 이 책에서는 자연에서 볼 수 있는 것들을 모델로 시스템을 구축하고자 하기 때문에, 균등한 무작위성이 항상 좋은 것은 아니다. 때로는 저울에 엄지손가락을 약간 올려야할 때도 있다.
난수의 비균등 분포를 만드는 것은 이 책 전체에서 유용하게 사용될 것이다. 예를 들어 9장의 유전 알고리즘에서는, 다음 세대에 DNA를 물려주기 위해 어떤 구성원을 선택해야 하는가에 대한 선택을 수행하기 위한 방법론이 필요하다. 이는 다윈의 적자생존(survival of the fittest) 개념과 유사하다. 진화하는 원숭이 집단이 있다고 가정해보자. 모든 원숭이가 번식할 기회가 균등하지 않다. 다윈의 자연 선택을 시뮬레이션 하려면, 무작위의 두마리의 원숭이를 부모로 선택할수는 없다. 더 “적합한” 원숭이가 선택될 가능성이 높아야 한다. 이를 적자생존 확률 이라고 할 수 있다.
여기서 잠시 멈춰 확률의 기본 원리를 살펴보면서 앞으로의 에제에서 더 정확한 단어를 적용할 수 있도록 하자. 먼저 single-event probability(단일 사건 확률) - 주어진 하나의 특정 사건이 발생할 확률에서부터 시작해보자. 확률에서, 결과(outcomes)는 무작위 프로세스에서 가능한 모든 결과를 의미하며, 사건(event)은 고려중인 특정 결과 또는 결과의 조합을 의미한다.
각 결과가 다른 결과와 똑같이 발생할 가능성이 있는 시나리오라면, 특정 사건이 발생할 확률은 해당 사건과 일치��하는 결과의 수를 잠재적 결과의 총 수로 나눈 값과 같다. 동전 던지기가 간단한 예제이다. 이는 앞면 또는 뒷면이라는 두가지 결과만 가능하다. 앞면이 하나뿐이므로, 동전이 앞면으로 나울 확률은 1을 2로 나눈 값인 1/2 또는 50%이다.
52장의 카드 덱을 준비한다. 이 덱에서 에이스를 뽑을 확률은 다음과 같다:
number of aces / number of cards = 4 / 52 = 0.077 ≈ 8%
다이아몬드를 뽑을 확률은 다음과 같다:
number of diamonds / number of cards = 13 / 52 = 0.25 = 25%
각 사건의 개별 확률을 곱하여 여러 사건이 순차적으로 발생할 확률을 계산할 수도 있다. 예를들어, 동전이 세 번 연속으로 앞면이 나올 확률은 다음과 같다:
(1/2) × (1/2) × (1/2) = 1/8 = 0.125 = 12.5%
이는 동전이 평균적으로 8번 중 한번은 3번 연속으로 앞면이 나온다는 것을 의미한다. 동전을 500번 연속으로 3번 던진다면, 평균 1/8, 약 63번의 확률로 3번 연속 앞면이 나올 것으로 예상할 수 있다.
Exercise 0.2
52장의 카드로 구성된 덱에서, 2번째 draw를 하기 전에 첫번째 draw를 다시 덱으로 섞을 때 2장의 에이스를 연속으로 뽑을 확률은 얼마인가? 첫번째 draw 이후 다시 섞지 않았다면 그 확률은 얼마나 될까?
random() 함수를 몇가지 방법으로 사용하여 코드에 확률 개념을 적용함으로써 비균등 분포를 만들 수 있다.
한가지 기법은 배열을 숫자로 채우고(반복가능), 배열에서 무작위 원소를 선택하고 그 선택에 따라 이벤트를 생성하는 것이다:
// 1, 3은 배열에서 2번 존재하므로, 2보다 자주 선택되게 만든다.
let stuff = [1, 1, 2, 3, 3];
// 배열에서 무작위 원소를 선택한다.
let value = random(stuff);
print(value);5개의 멤버로 구성된 배열은 2개의 1이 있으므로, 이 코드를 실행하면 5번 중 2번, 즉 40%의 확률로 1을 출력할 것이다. 마찬가지로 2가 출력될 확률은 20%, 3이 출력될 확률은 40% 이다.
또한 임의의 숫자를 요청하고 (간단하게 0에서 1 사이의 임의의 부동소수점 값만 고려해보자) 그 임의의 숫자가 특정 범위 내의 있는 경우만 이벤트가 발생하도록 허용할수도 있다. 예를들어:
let probability = 0.1;
let r = random(1);
if (r < probability) {
print("Sing!");
}0에서 1 사이의 부동 소수점 숫자 중 1/10이 0.1보다 작으므로, 이 코드는 10%의 시간만 노래로 이어진다.
동일한 접근 방식을 사용하여 여러 결과에 다른 가중치를 적용할 수 있다. 예를들어 노래는 60%의 확률로, 춤은 10%의 확률로, 잠은 30%의 확률로 발생하기를 원한다고 가정해보자. 다시 말하지만, 0에서 1 사이의 임의의 숫자를 선택하고 그 숫자가 어디에 속하는지 확인할 수 있다.
- 0.0에서 0.6 (60%) -> 노래하기
- 0.6에서 0.7 (10%) -> 춤추기
- 0.7에서 1.0 (30%) -> 잠자기
let num = random(1);
if (num < 0.6) {
print("Sing!");
} else if (num < 0.7) {
print("Dance!");
} else {
print("Sleep!");
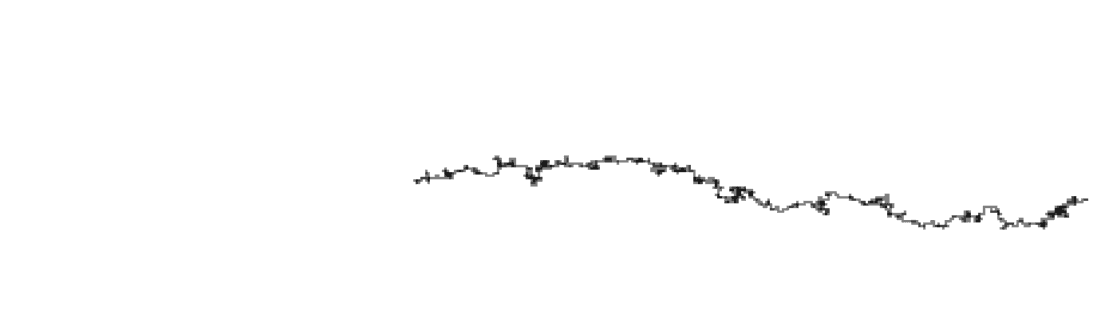
}이제 이 방법론을 random walker에 적용하여 특정 방향으로 이동하는 경향이 있도록 해보자. 다음은 다음과 같은 확률을 가진 Walker 객체의 예제이다.
- 위로 이동할 확률 : 20%
- 아래로 이동할 확률 : 20%
- 왼쪽으로 이동할 확률 : 20%
- 오른쪽으로 이동할 확률 : 40%
Example 0.3 : A Walker That Tends to Move to the Right
step() {
let r = random(1);
// 40%의 확률로 오른쪽으로 움직인다.
if (r < 0.4) {
this.x++;
} else if (r < 0.6) {
this.x--;
} else if (r < 0.8) {
this.y++;
} else {
this.y--;
}
}
이 기법의 또다른 일반적인 용도는 코드에서 산발적으로 발생하기를 원하는 이벤트의 확률을 제어하는 것이다.
예를들어, 일정한 시간 간격 (매 100 프레임마다) 새로운 random walker가 시작되는 스케치를 만든다고 가정해보자.
random()을 사용하면, 대신 새로운 워커가 시작되는 확률을 1%로 지정할 수 있다.
최종 결과는 동일하지만 (평균적으로 100프레임 중 1프레임마다 새로운 워커가 시작됨), 후자는 우연성을 포함하며 더 역동적이고 예측할 수 없는 느낌을 준다.
Exercise 0.3
동적 확률로 랜덤 워커를 생성한다. 예를들 마우스 방향으로 움직일 확률을 50%로 설정할 수 있을까? p5.js에서
mouseX와mouseY를 사용하면 현재 마우스 위치를 가져올 수 있다는 것을 기억해보자.